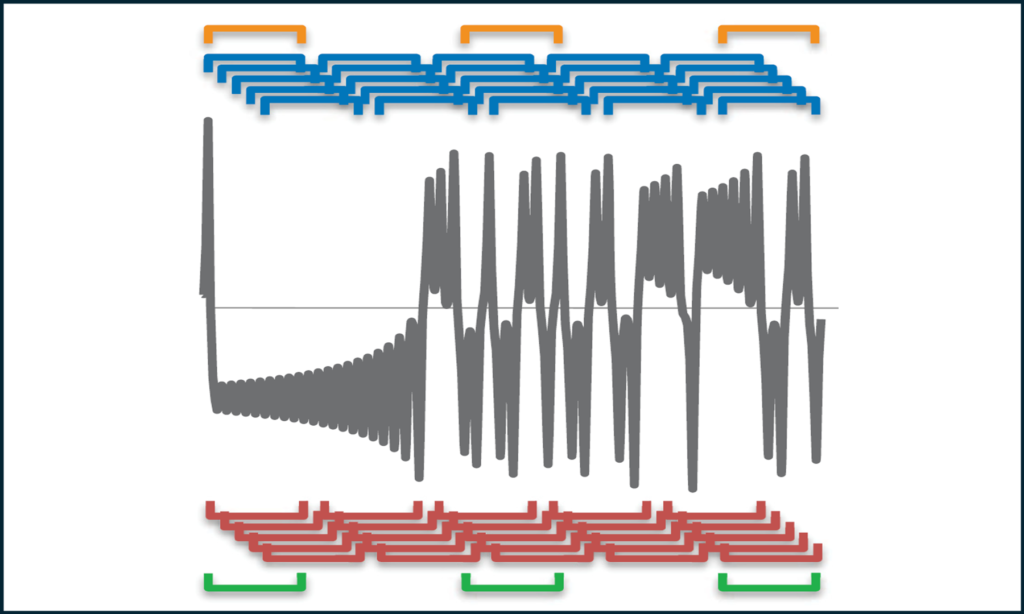
Flow data from simulations and experiments have never been more plentiful. We develop and employ methods to extract knowledge and simplified models from data.  For example, we have contributed to the theory, algorithms, and application of spectral proper orthogonal decomposition (SPOD), which we have shown is better suited than popular alternatives for identifying organized structures hidden within turbulent flows.  Current work includes using SPOD modes to obtain predictive models, formulating data-driven versions of various linear stability methods, and formulating new data-driven methods tailored for specific objectives.

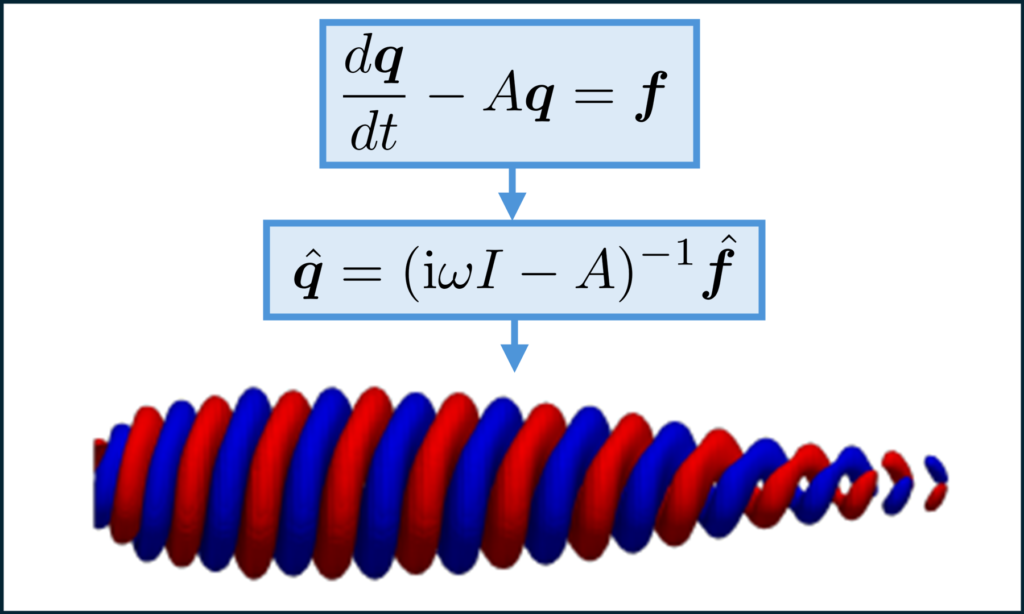
Models based on simplified forms of the governing Navier-Stokes equations and/or phenomenological descriptions of physical processes complement data-driven methods by offering superior interpretability and generalizability. We develop theoretical and computational tools that enable physics-based reduced-complexity models for turbulent flows.  Examples include modeling energy amplification mechanisms and the resulting coherent structures in turbulent flows using resolvent analysis and predicting resonance phenomena in a variety of flows using linear stability analysis.

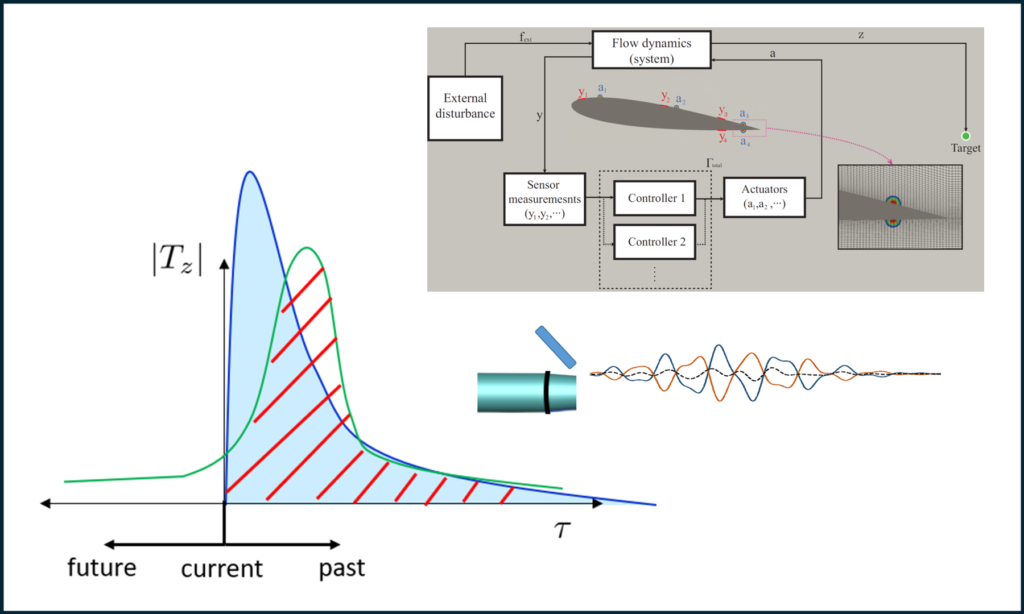
The ability to control turbulent flows via subtle real-time actuation would help achieve numerous engineering objectives, including reducing drag-induced fuel consumption and emissions from air and ground vehicles, mitigating the adverse health effects of excessive noise exposure from wind turbines and jet engines, and improving the aerodynamic performance and maneuverability of aircraft. We have developed a new framework for the real-time estimation and control of turbulent flows using resolvent analysis that offers several advantages over standard methods, including improved accuracy and reduced computational cost.  We are applying these tools to several problems, including suppressing vortex shedding in the wake of an airfoil and mitigating jet noise by canceling noise-emitting coherent structures.

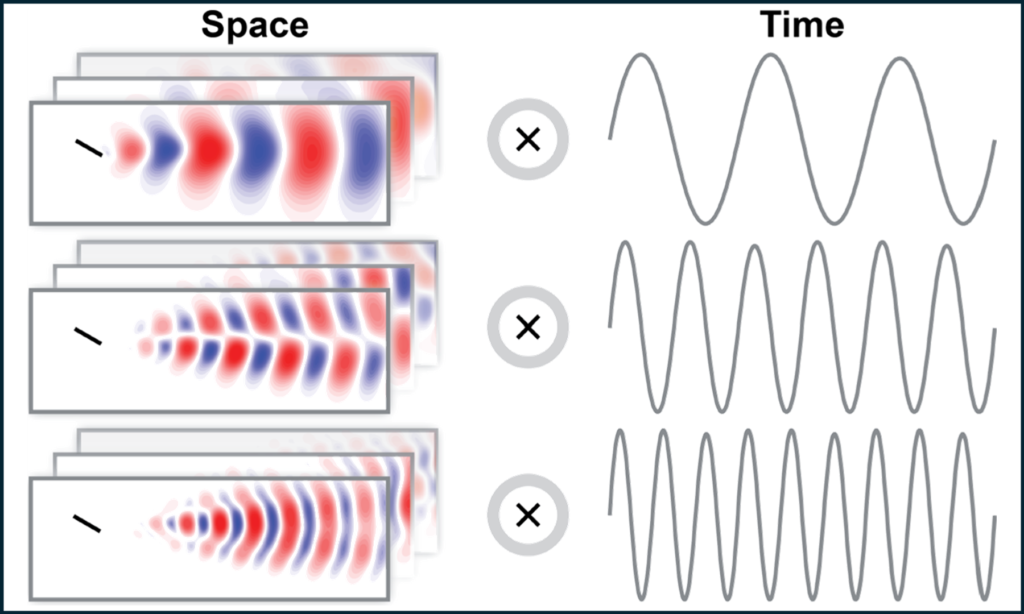
High-fidelity numerical simulations of turbulent flows are computationally expensive, making reduced-order models that can provide accurate approximations of a flow at a lower cost highly desirable. Predictive nonlinear reduced-order models for fluid systems are typically obtained using a reduced basis of spatial modes weighted by time-varying amplitude coefficients.  We are developing a family of alternative methods in which the basis functions themselves depend on both space and time.  Due to the superior representation power of space-time basis functions and improved physical consistency with the space-time dynamics of fluid flows, this approach has the potential to outperform and overcome well-known limitations of standard reduced-order models for turbulent flows.  Ultimately, improved nonlinear models could enable improved estimation, control, design optimization, and physical understanding of countless engineering systems involving turbulent flow.

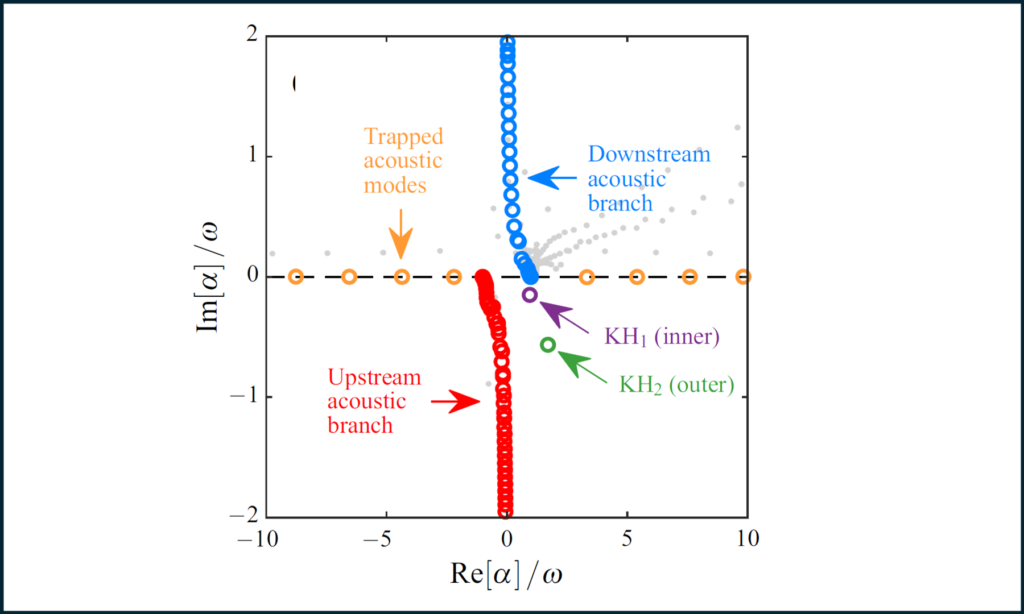
The growth of small disturbances, the topic of hydrodynamic stability theory, is an important process both in the transition of laminar flows to turbulence and in the emergence of coherent structures in turbulent flows. We develop new methods and computational tools to expand the applicability of this theory.  Examples include a spatial-marching method to compute the evolution of disturbances at low cost in slowly varying flows (like mixing and boundary layers), a novel statistical theory of transient growth, and a new algorithm to enable resolvent analysis of three-dimensional flows.

One of our primary application areas is jet aeroacoustics, where the goal is to understand, predict, and ultimately reduce the noise produced by turbulent jets. We apply many of the previously mentioned methods to model the dynamics and acoustics of subsonic and supersonic jets, with special attention toward modeling and controlling the large-scale wavepacket structures responsible for much of the emitted noise.  We also seek to understand and predict resonant phenomena that produce intense tonal noise in several scenarios, including shock-containing jets, impinging jets, and jet-wing interaction.

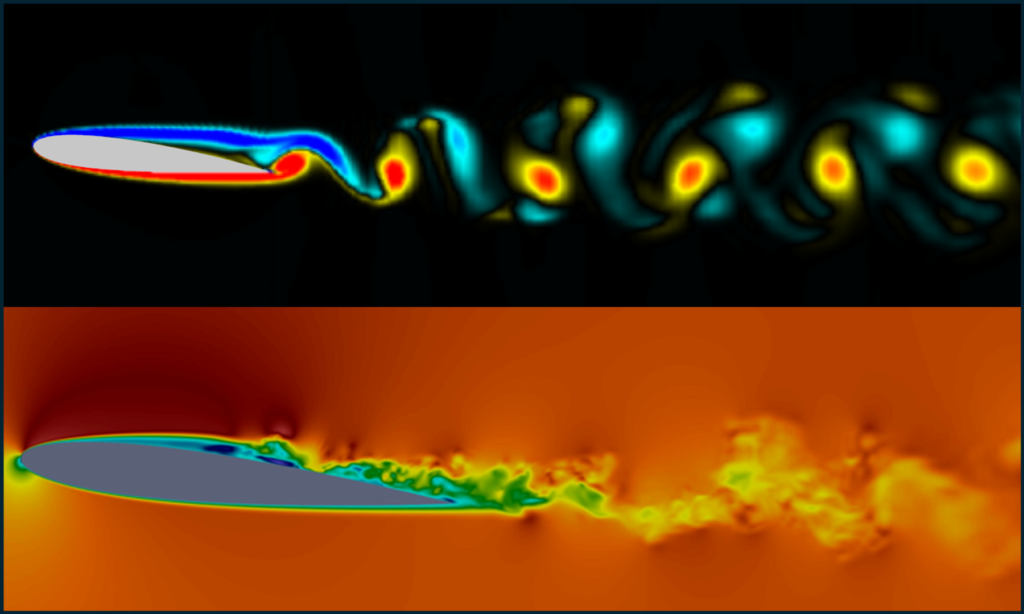
Large-scale structures, such as vortices shed from the leading or trailing edge of a wing, significantly impact aerodynamic quantities of interest like lift and drag. We develop models and control strategies for these coherent structures, with a focus on turbulent boundary layers and wakes.

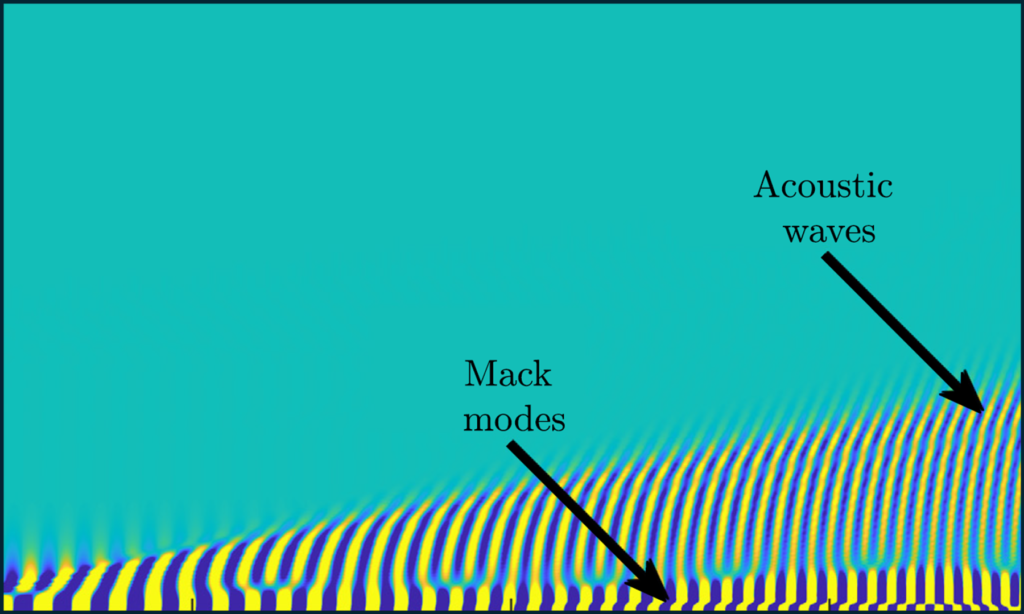
The state of a boundary layer – laminar or turbulent – critical impacts engineering quantities of interest, including drag, structural loading, and surface heating on air, ground, and naval vessels. Focusing on high-speed boundary layers typical of supersonic or hypersonic aircraft, we are developing new probabilistic transition models using a novel theory of transient growth along with linear and nonlinear stability methods.  Rather than seeking a definite transition point, which is inconsistent with the sensitivity and intermittent nature of transitional flow, the new model will take a statistical description of environmental disturbances as input and predict the expected (mean) transition point and the probability of observing transition at each downstream position along the boundary layer.  The new models could lead to improved scientific understanding of transition and more robust engineering design.